3D Coordinates System

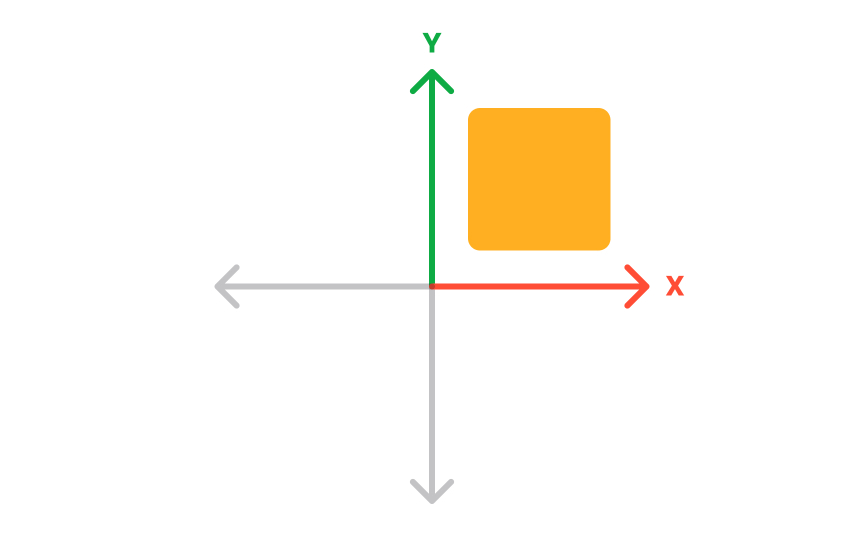
A 2D coordinate system is formed by X and Y axes — two lines drawn at right angles to each other on a flat surface. Each axis has a unit of length or distance, for example, centimeters or inches. Any point within the coordinate system has a pair of coordinates describing a distance relative to both the x and y axes (x,y). The point where the axes cross is called the origin, and the value of both x and y there is zero (0,0). A 2D system can describe points on a flat plane, and it only has width and length.^[1]

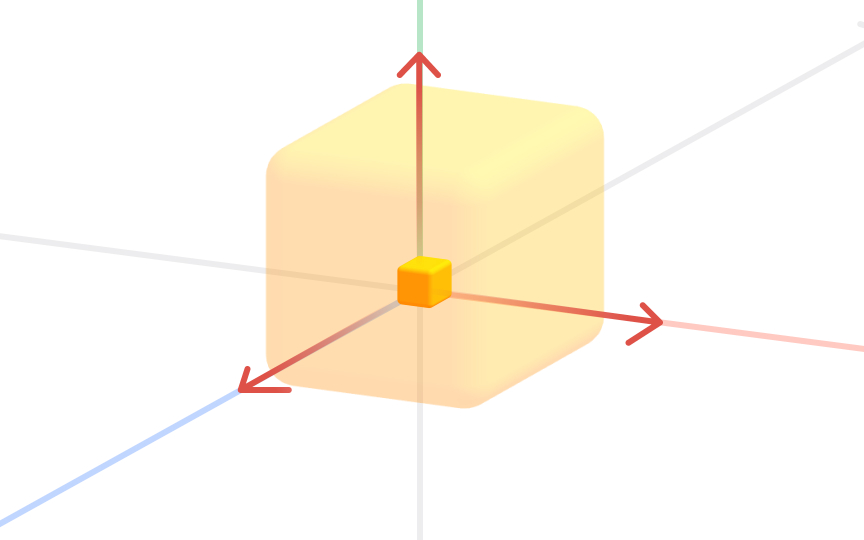
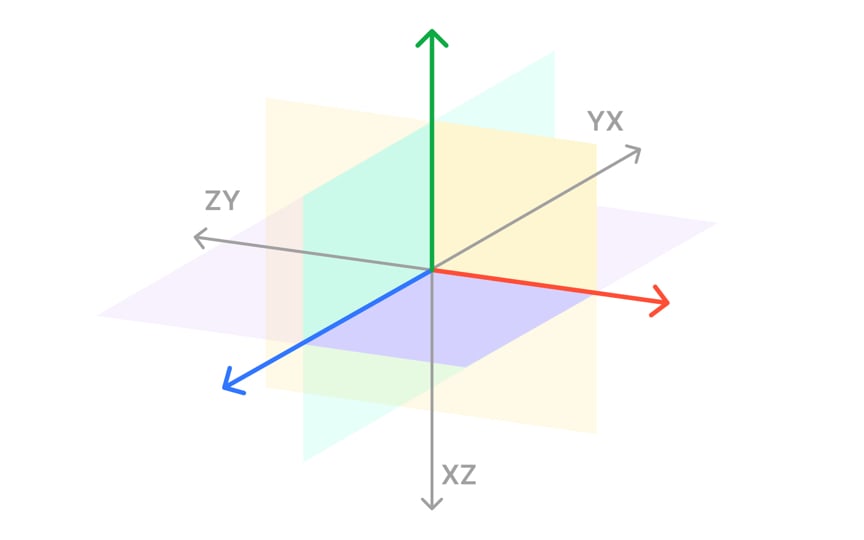
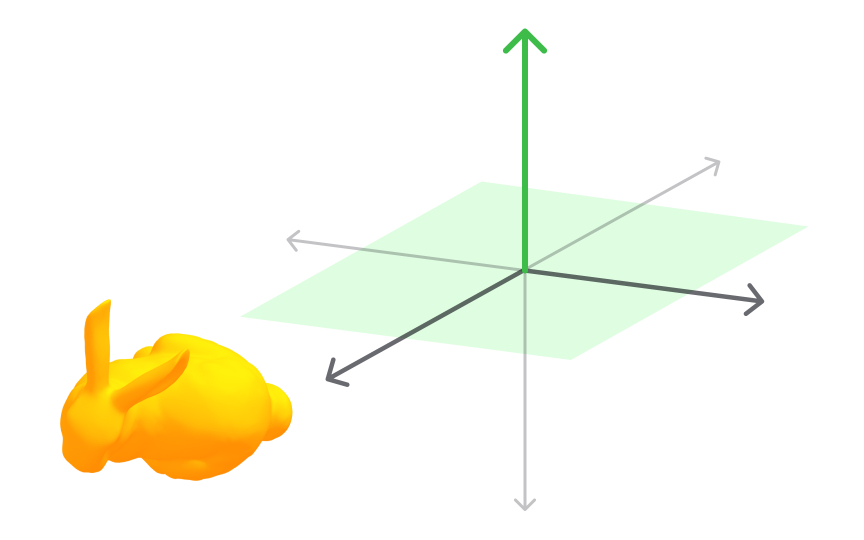
2 axes are not enough to describe the world that surrounds us. For that, we need the third dimension — depth — and a 3D coordinate system formed by three mutually perpendicular vectors crossed at the origin — the x-axis, the y-axis, and the z-axis. In this case, you can imagine the point as being somewhere within a rectangular box.^[2]

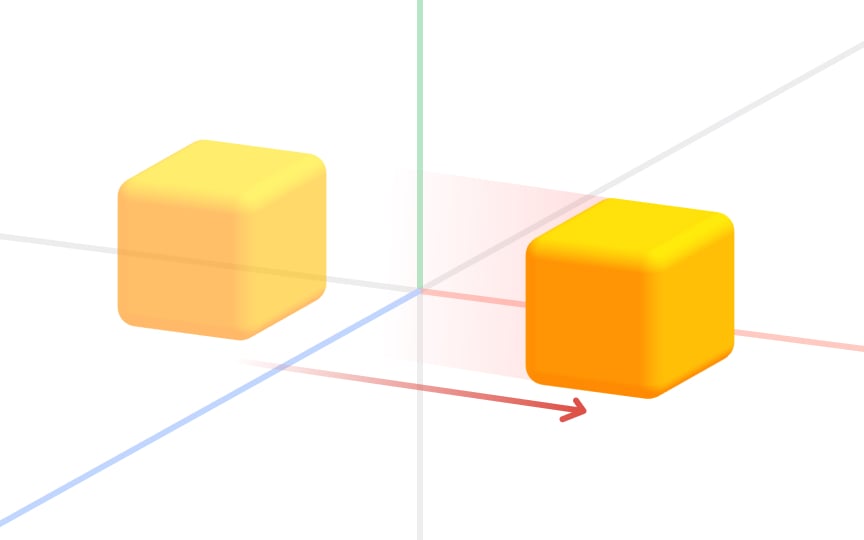
3D models can be viewed in specialized software suites from any angle, where they can be easily manipulated. Processes of manipulating objects in a coordinate system are called transformations. There are 4 basic types of transformations: translation, rotation, reflection, and dilation. Translation in a geometrical sense means moving an object without rotating or resizing. To translate a shape means to move each of its points at the same distance in the same direction.^[3]

Scaling — also called dilation — allows us to resize objects relative to a reference point. To do the same, we draw a straight line from the point and move each point of the object along this line.

The distance the points move depends on the scale factor:

• If it's larger than 1, the object will be larger than the original
• If it's less than 1, the object will be smaller
• If it's negative, the object will be on the opposite side of the reference point compared with the original

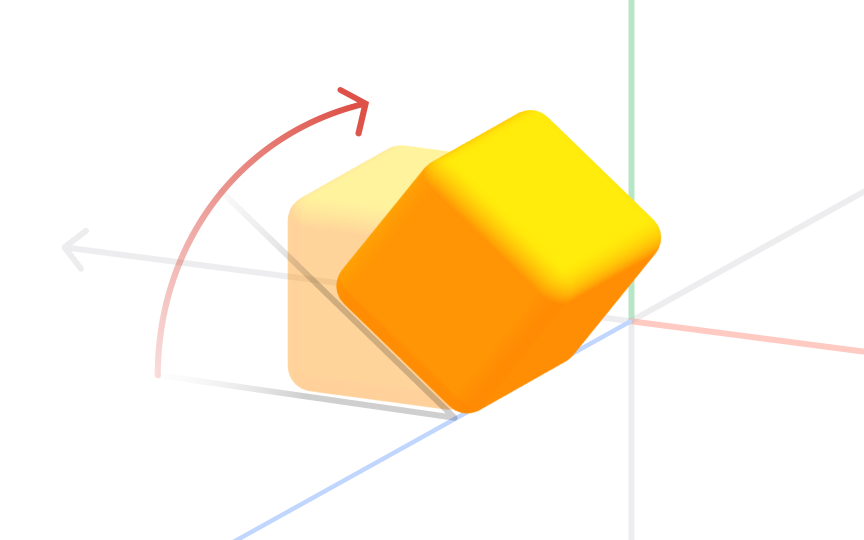
Rotation means turning an object around a chosen center, while the distance from the center to any point of the object stays the same. The direction of rotation can either be clockwise or anticlockwise. The number of rotations made is called the angle of rotation. For any rotation, we need to specify the center, the angle, and the direction of rotation.

A coordinate plane is formed by the intersection of 2 axes. As there are only 2 axes in a 2-dimensional system, there's only one coordinate plane — the XY plane. But a 3-dimensional coordinate system has 3 coordinate planes — XY, ZX, and YZ planes, containing 2 axes each.^[4] However, it can be tricky to represent these 3 dimensions in the 2 dimensions of a screen or a piece of paper.

3D modeling software allows you to rotate the view of a model dynamically, as a single perspective may not show details hidden from view. The top view looks straight down at the XY plane, while the bottom view looks at the same plane but from the opposite side.^[5]

The front view looks at the plane defined by the X and the Z axes, and the back view looks at the same plane but from a totally opposite point of view. Think about how you can see the front of the house standing in front of it and its back if you walk around and look at it from the opposite side.

The side view allows you to look at the plane formed by the Y and the Z axes. Usually, when using a one-perspective view, you cannot draw on other planes properly. The view from the left and right sides can differ, just as a person's profile looks different from left and right. 

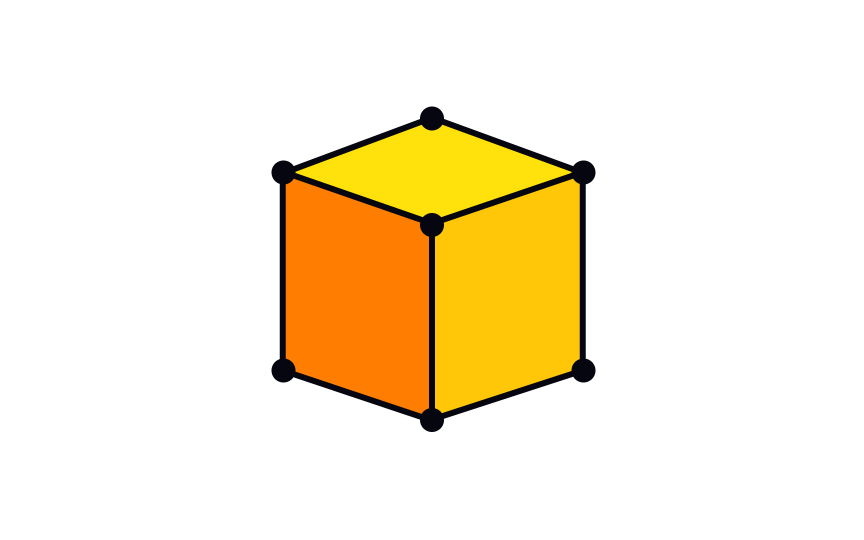
3D models are one of the essential building blocks of 3D computer graphics. The most common type is polygonal models — 3D shapes made up of 2D shapes joined at certain angles. Like the geometric shapes you learned about in middle school, they comprise faces, edges, and vertices.^[6]

A face is any of the individual flat surfaces that form parts of the boundary of a solid object. 2D shapes don't have faces as they lie in one plane. Connecting multiple faces allows us to create 3D shapes like cubes, a 6-faced regular hexahedron.

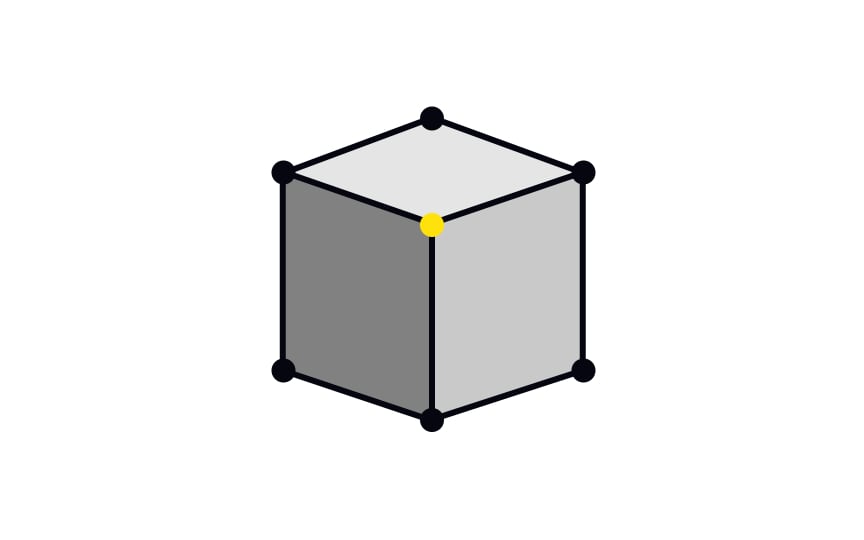
A vertex is a point where two or more line segments meet. For example, a cube has 8 vertices. 2D shapes have vertices too, but we often call them corners — a cube comprises squares, and each square has 4 vertices. Sometimes, vertices are also called corners, a type of vertice where only 2 lines meet — they're basically vertices of 2D shapes.

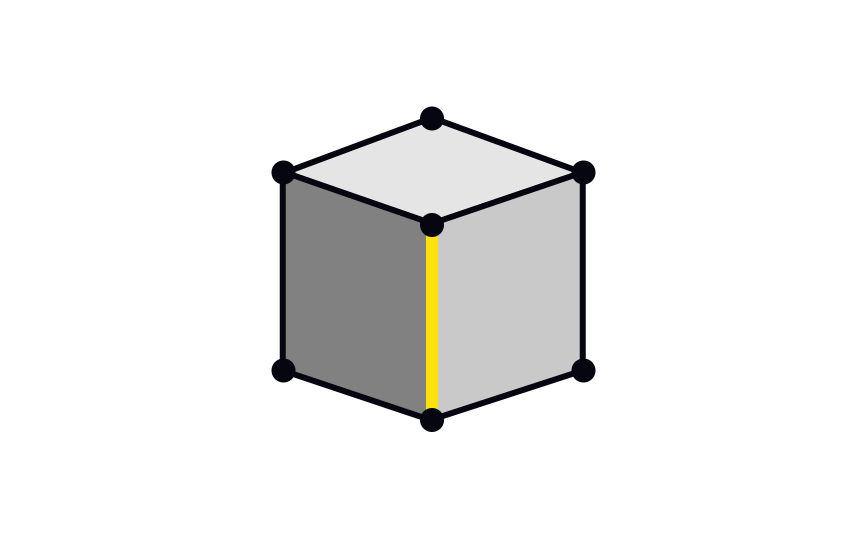
When discussing 3D shapes, an edge is a line segment where two faces meet. An edge of a polygon joins one vertex to another. For example, our old friend cube has 12 edges. In the context of 2D shapes, the correct term is "sides." We'll let you guess how many sides a square has.